Au cours des dernières étapes, nous avons constaté que les populations sont très dynamiques et que nous pouvons aborder leur taille et leur croissance à l’aide de différentes équations et calculs. Dans cette étape, nous nous penchons plus en détail sur cette compréhension et découvrons que, par exemple, la propagation d’une maladie peut être interrompue par la vaccination d’un certain nombre de personnes.

Conditions d’état d’équilibre et taux de reproduction de base

Dans de nombreuses situations, nous manquons de données suffisantes pour analyser le comportement du modèle, mais nous pouvons étudier les propriétés essentielles du modèle en nous basant sur les équations différentielles. Elles décrivent l’évolution des quantités, et nous pouvons étudier leurs conditions d’équilibre en les réglant à zéro. Par exemple, nous pouvons étudier les conditions d’équilibre du compartiment infectieux $$I$$.

$$\frac{dI}{dt} = \beta IS - \mu I - \delta I = 0 {\color{red}{→}} \beta IS = (\mu + \delta)I {\color{red}{→}} S = \frac{(\mu + \delta)}{\beta}$$

Équation 1

Le compartiment $$I$$ atteint un équilibre endémique lorsque le nombre de personnes exposées atteint une taille particulière, qui dans l’exemple ci-dessus est $$S = (\frac{0.05+0.2}{0.001}) = 250$$. Une autre interprétation de cette condition d’état d’équilibre est que le nombre d’individus exposés au début de l’épidémie doit être supérieur à une certaine quantité fixe si l’infection doit se propager et persister dans la population. Sur l’image une simulation du compartiment infectieux est présentée avec différentes tailles de populations exposées au début. Nous voyons qu’en dessous de 250 individus exposés, la transmission ne décollera pas.

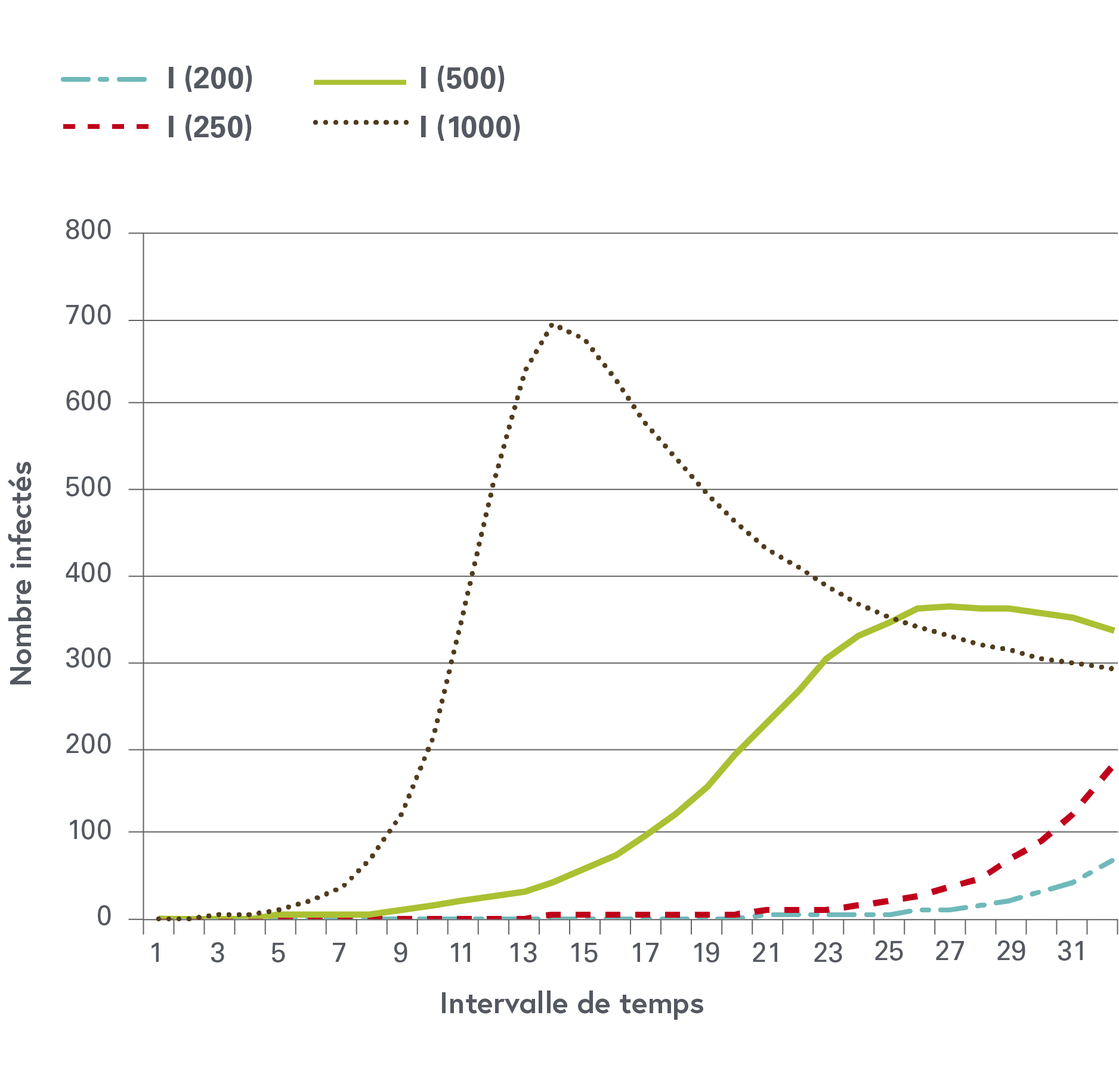
Image 1 : Nombre d’individus infectieux avec un nombre variable de sujets exposés (200, 250, 500 and 1000)

© Jakob Zinsstag

Le taux de reproduction de base (BRR ou $$R_0$$) est défini comme le nombre moyen d’infections secondaires produites lorsqu’un individu infecté est introduit dans une population hôte où chaque hôte est exposé. Le $$R_0$$ décrit la propagation potentielle d’une pathologie infectieuse et sa régulation dans une population hôte. Si le $$R_0$$ est supérieur à 1, la pathologie continue de se propager. Si $$R_0$$ est inférieur à 1, la pathologie ne sera pas maintenue mais disparaîtra. On peut repartir de l’équation 1 qui décrit le changement des individus infectieux.

$$\frac{dI}{dt} = \beta IS - \mu I - \delta I {\color{red}{→}} \beta S ≥ (\mu + \delta) {\color{red}{→}} \frac{\beta S}{\mu + \delta} ≥ 1 = R_e$$

Équation 2

Le $$R_0$$ est supérieur à 1, et donc la pathologie continue de se propager si $$\beta S$$ est supérieur à $$(\mu I + \delta) $$. Son rapport est appelé rapport effectif de reproduction ($$R_e$$) et varie en fonction du nombre d’hôtes exposés. Au début d’une épidémie, tous les individus sont exposés et $$S = N$$. Le taux de reproduction de base est alors exprimé comme suit

$$R_0 = \frac{\beta N}{\mu + \delta} {\color{red}{→}} N = R_0 \frac{(\mu + \delta)}{\beta}.$$

Équation 3

Si nous résolvons ce problème pour $$N$$ nous obtenons à nouveau le seuil de population susmentionné requis pour qu’une épidémie commence. Une application très utile du BRR est de rechercher la couverture vaccinale minimale nécessaire pour éradiquer une pathologie. Si la couverture vaccinale est de $$p$$, le nombre d’hôtes exposés restants devient $$(1 - p)N$$. Le niveau critique de vaccination peut être calculé comme suit

$$R_0 (1 - p_c) = \frac{\beta N (1 - p_c)}{(\mu + \delta)} = 1 {\color{red}{→}} R_0 (1 - p_c) = 1$$

$$p_c = 1 - \frac{1}{R_0}.$$

Équation 4

Lizenz