Here you find the solution to the exercise of the previous step. If desired, you may download a completed spreadsheet.

The formulas should be:

$$S_{(T+1)}$$= B2 + ($F$2 * (B2+C2+D2)) - ($E$2 * B2 * C2) - ($F$2 * B2)
$$I_{(T+1)}$$= C2 + ($E$2 * B2 * C2) - ($F$2 * C2) - ($G$2 * C2)
$$R_{(T+1)}$$ = D2 + ($G$2 * C2) - ($F$2 * D2)

The graph should look like this:

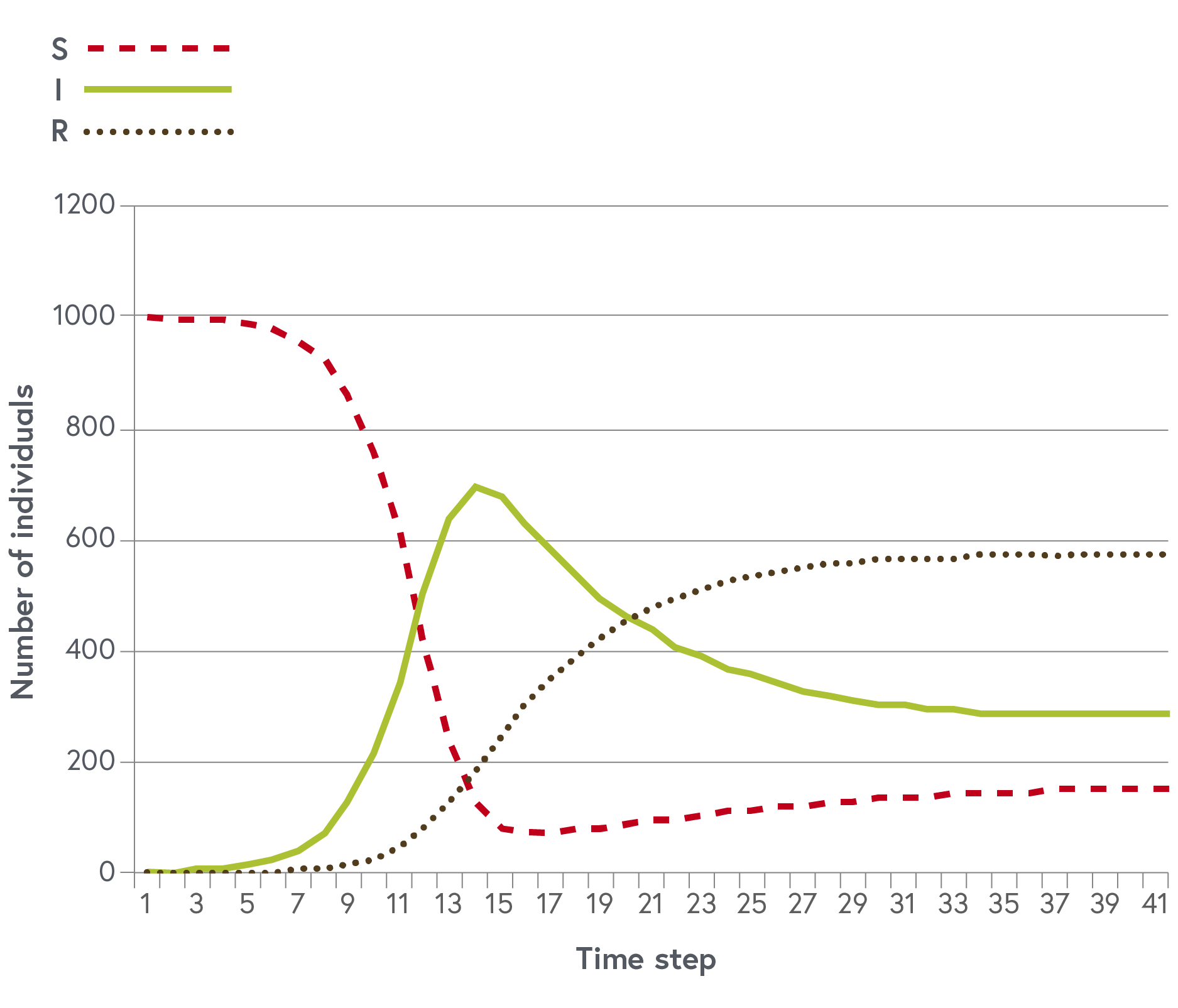Time dependent changes in the numbers of susceptible, infectious and recovered individuals.

© Jakob Zinsstag

Answer on the dynamics:

We observe an initial epidemic peak and then an on-going low level of transmission.

Answer on shortfalls:

The formula works with non-integer numbers. In principle, there should only be integers if we assume individuals. This problem can be overcome if we assume that we deal with large numbers, for example, a million people instead of one thousand. The model uses discrete time steps, which is a good approximation if the time steps are short (like days) but performs poorly if the time steps represent years.

Lizenz

Downloads