Vous trouverez ici la solution de l’exercice de l’étape précédente. Si vous le souhaitez, vous pouvez télécharger une feuille de calcul remplie.

Les formules devraient être :

$$S_{(T+1)}$$= B2 + ($F$2 * (B2+C2+D2)) - ($E$2 * B2 * C2) - ($F$2 * B2)
$$I_{(T+1)}$$= C2 + ($E$2 * B2 * C2) - ($F$2 * C2) - ($G$2 * C2)
$$R_{(T+1)}$$ = D2 + ($G$2 * C2) - ($F$2 * D2)

Le graphique devrait ressembler à :

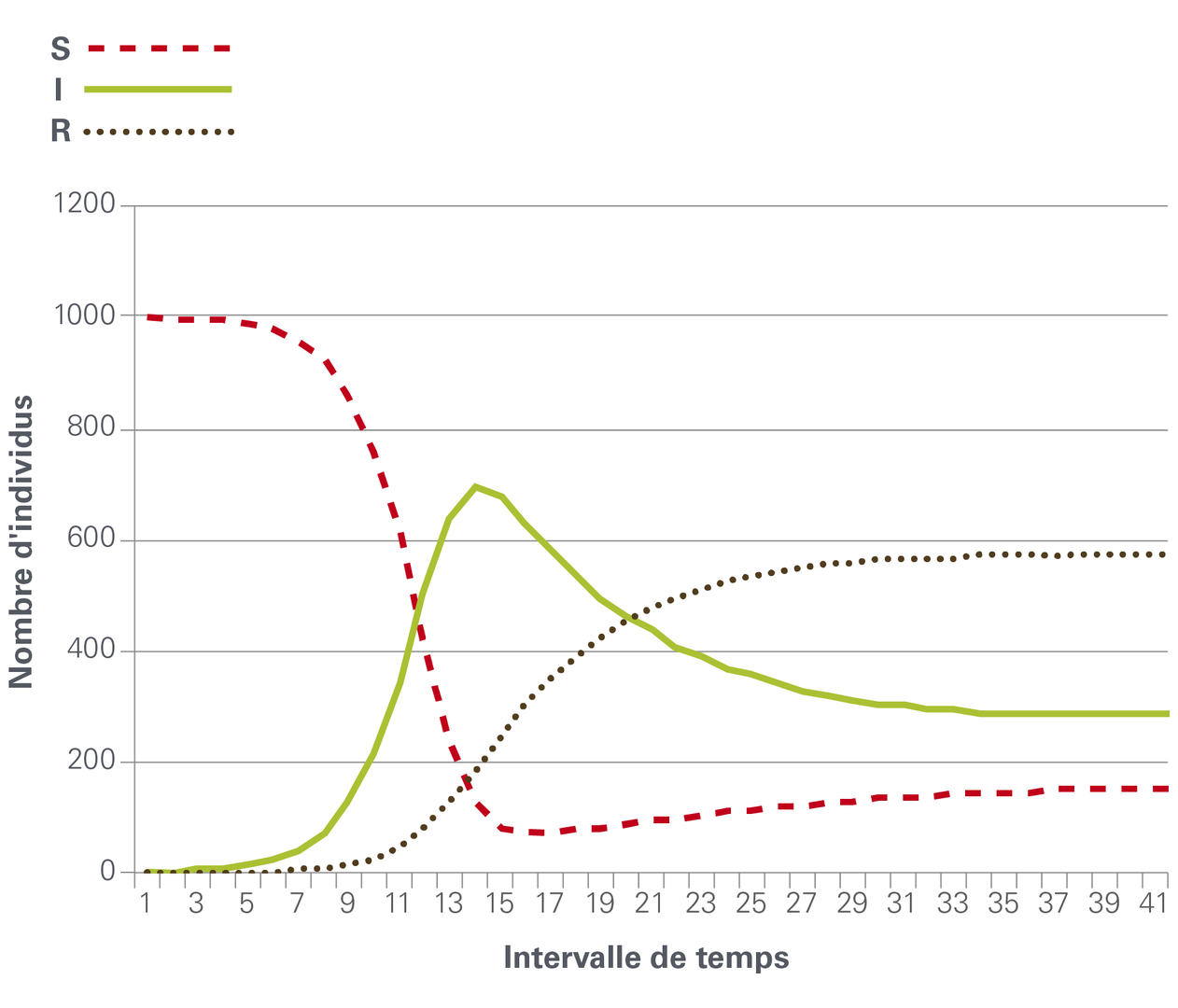
Changements du nombre de personnes exposées, infectieuses et rétablies en fonction du temps.

© Jakob Zinsstag

Réponse sur la dynamique :

Nous observons un pic d’épidémie initial, puis un faible niveau de transmission continu.

Réponse sur les insuffisances :

La formule fonctionne avec des nombres non entiers. En principe, il ne devrait y avoir de nombres entiers que si nous considérons des individus. Ce problème peut être résolu si l’on considère que nous avons affaire à un grand nombre, par exemple, un million de personnes au lieu d’un millier. Le modèle utilise des intervalles de temps distincts, ce qui est une estimation appropriée si les intervalles de temps sont courts (comme les jours) mais fonctionne mal si les intervalles de temps représentent des années.

Lizenz

Downloads