Les populations sont dynamiques. Elles sont influencées par divers événements, comme par exemple les naissances et les décès. Une maladie peut également modifier le nombre d’individus dans une population. Mais comment modéliser une population dynamique ? Examinons cette question dans le cadre d’une approche One Health. Si votre navigateur rencontre des problèmes d’affichage des formules mathématiques, vous trouverez en pièce jointe le PDF de cet article ci-dessous

Les populations sont dynamiques.

Le phénomène des pathologies infectieuses au sein des populations est avant tout un processus dynamique à tous les niveaux. La population hôte exposée change continuellement en raison d’événements tels que la naissance, l’immigration, l’émigration et la mort. La population parasitaire croît dans l’hôte, est détruite par le système immunitaire ou demeure à faible densité dans les hôtes réservoirs. La somme de tous les événements peut être exprimée en tant que réservoir ou compartiment, tel que représenté ici avec l’exemple d’une population hôte (voir image 1). La taille de ce compartiment peut augmenter, diminuer ou osciller. Même si la taille totale est stable, elle peut être extrêmement dynamique. Les processus ci-dessus se déroulent indépendamment mais simultanément. Ils peuvent être exprimés en termes de population totale par unité de temps, c’est-à-dire en taux de natalité annuel ou instantané par habitant $$b$$ ou en taux de mortalité annuel par habitant $$m$$. Ces taux eux-mêmes peuvent être constants ou dynamiques. Les populations peuvent augmenter ou diminuer à un rythme constant.

Image 1 : organigramme démographique simple

© Jakob Zinsstag

La dynamique des populations peut être modélisée

La dynamique des populations peut être quantifiée en termes de processus déterministes ou stochastiques. On pourrait dire que les modèles sont toujours imparfaits en raison de la complexité de la nature. Néanmoins, les processus partiels peuvent très bien être modélisés avec une très grande précision. Au mieux, les modèles sont des aides à la réflexion ou des cadres pour la prise de décision. Il est essentiel de bien identifier le processus que nous voulons décrire. Pour ce faire, nous devrions établir ses différents éléments sous forme d’organigramme (voir image 1). La règle de base est de ‘modéliser ce que l’on peut compter’. Pour chaque article comptabilisable, nous dessinons une boîte. Les flèches sont utilisées pour relier les compartiments et indiquer la direction des transitions spécifiques telles que les naissances, les décès ou l’infection. L’organigramme qui en résulte peut se traduire en équations mathématiques. Dans un premier temps, une équation est écrite pour chaque compartiment.

Image 2 : la population isolée $$P$$

© Jakob Zinsstag

En reprenant notre premier exemple, dans l’image 2, nous décrivons à nouveau l’organigramme de l’image 1, cette fois en supposant que la population est isolée et qu’il n’y a ni immigration ni émigration. Si on multiplie les taux par habitant par la taille de la population, on obtient les taux nets de natalité $$bP$$ ou les taux nets de mortalité $$mP$$. Si l’intervalle de temps choisi approche zéro, la dynamique de la population totale peut être exprimée sous la forme d’un dérivé $$\frac{dP}{dt}$$. Le taux instantané de changement démographique - qui est proportionnel à la taille totale de la population (voir équation 1) - peut être écrit comme une équation différentielle (voir équation 2). Le différentiel $$\frac{dP}{dt}$$ est la déclivité de la fonction de démographie $$P(t)$$ dans le temps :

$$\frac{dP}{dt} ≈ P$$

Équation 1

$$\frac{dP}{dt} = +bP - mP {\color{red}→} \frac{dP}{dt} = (b - m)P$$

Équation 2

L’équation 2 décrit l’organigramme de l’image 2 mais ne nous donne aucune autre information sur la taille de la population à un moment donné. Ainsi, nous devons exprimer la relation en termes de population totale $$P$$ selon la naissance et la mortalité. Ceci peut être réalisé par une solution analytique de l’équation 2, en supposant que $$b$$ et $$m$$ sont constants.

$$\frac{dP}{dt} = (b - m)P {\color{red}→} \frac{dP}{P} = (b - m)dt {\color{red}→} ∫\frac{dP}{P} = ∫(b - m)dt {\color{red}→} $$
$$ ln P = (b - m)t + c {\color{red}→} P = e^{(b - m)t + c}$$

Équation 3

L’équation 3 est obtenue par l’intégration de l’équation 2 et exprime maintenant la population $$P$$ en tant que fonction de $$b$$ et $$m$$. $$C$$ est une constante qui peut être convertie en inscrivant la taille de la population au moment $$0$$. Ainsi, le terme dépendant du temps est zéro et l’équation peut être réécrite comme suit

$$P = P_0e^{(b-m)t}$$

Équation 4

Dans l’image 3, la dynamique d’une population $$ P_0 = 100$$ à l’année $$0$$ est tracée pour un taux de mortalité de $$m = 0.05$$ par an et un taux de natalité $$b = 0.15$$ par an seulement et pour la population totale $$P$$ (naissance-mort). La pente $$\frac{dP}{dt}$$ est ajoutée à la courbe en tant que ligne pointillée. Ce cas simple a une solution analytique, mais souvent des équations différentielles plus complexes ne peuvent pas être intégrées en utilisant des méthodes algébriques. Dans de tels cas, des programmes informatiques sont utilisés pour ajuster de manière itérative les paramètres aux données observées et produire une solution numérique de l’équation. Les paramètres du modèle ne sont pas toujours constants. Par exemple, la mortalité dépend de l’âge. Les plus jeunes meurent plus fréquemment que les plus âgés. Les paramètres peuvent également dépendre de la densité, ce qui signifie que les paramètres sont eux-mêmes à nouveau des fonctions de la population.

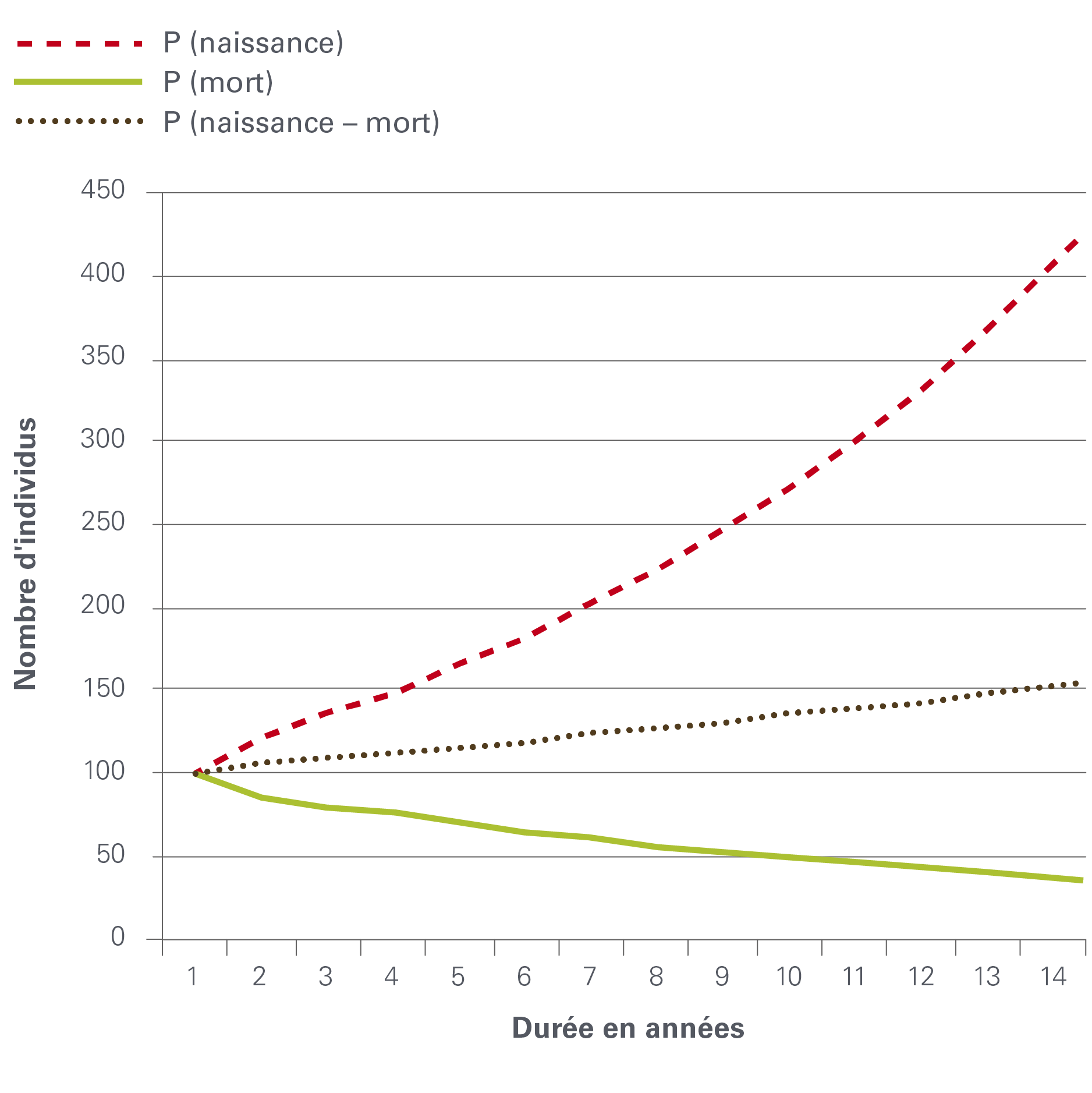
Image 3 : dynamique démographique avec taux de mortalité et de natalité en tant que processus indépendants

© Jakob Zinsstag

Modéliser des populations structurées

Les populations peuvent être divisées par sexe et tranche d’âge. L’image 4 montre un exemple illustrant un modèle structuré par âge et par sexe d’un cheptel bovin en Mongolie. $$x$$ sont des femelles qui donnent naissance et $$y$$ sont des mâles.

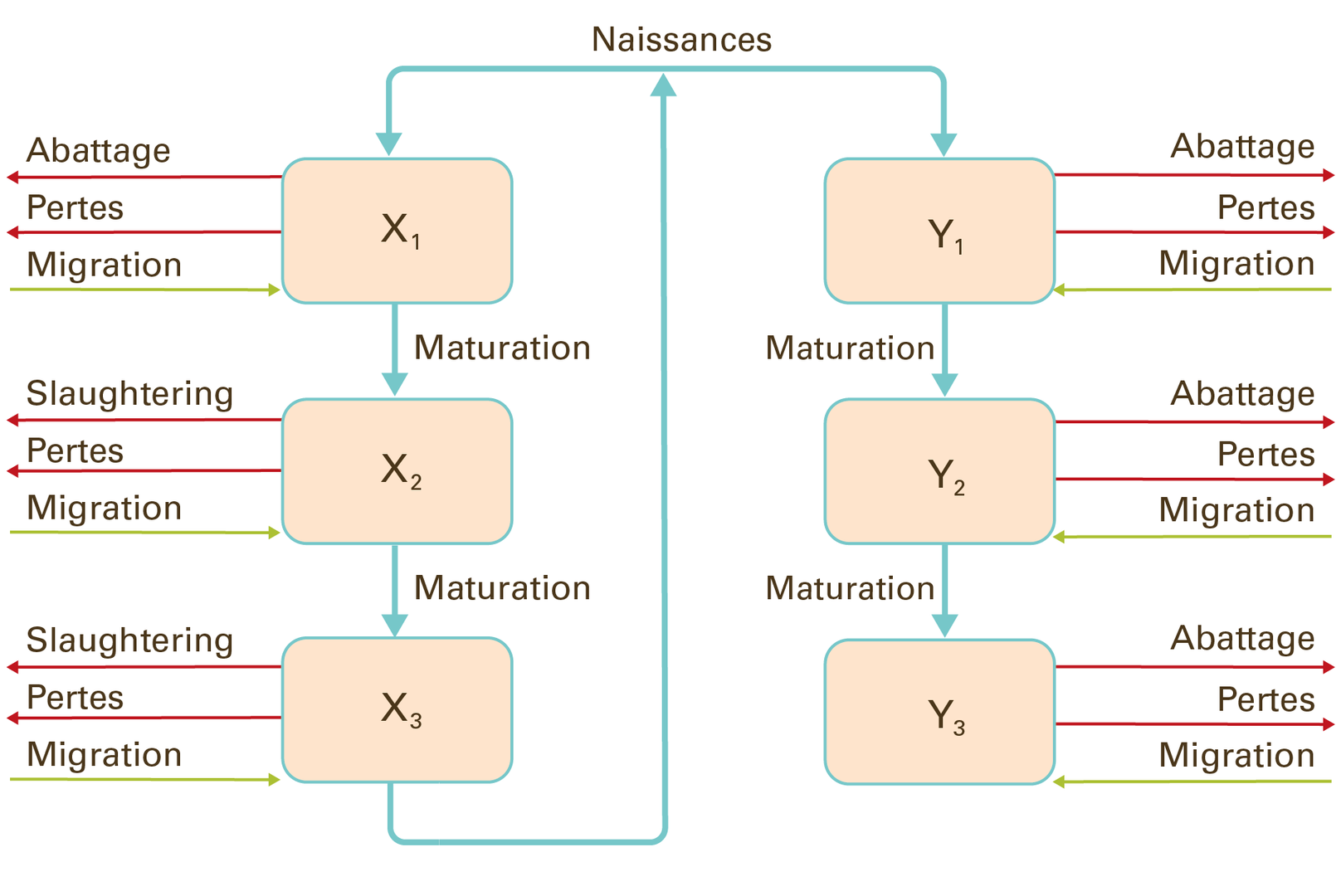
Image 4 : modèle démographique structuré par âge et sexe d’une population bovine

© adapté de Shabb et al. 2013, 280-288.

Ces modèles peuvent être simulés à l’aide d’équations différentielles ou de différence. Ils peuvent également être modélisés à l’aide de modèles matriciels. Nous introduisons ici le principe de la matrice de Leslie qui est largement appliqué dans la dynamique des populations. Nous suivons l’excellente introduction de Vandermeer et Goldberg au sujet de l’écologie des populations (Vandermeer et Goldberg 2008, 280pp).

Les différentes classes d’une population ne sont plus considérées comme une valeur unique (scalaire) mais peuvent être considérées comme un vecteur appelé vecteur population $$N$$. Dans cet exemple, nous considérons trois groupes d’animaux femelles : les jeunes, les sub-adultes et les adultes (reproductrices). Ce vecteur est multiplié par une matrice de projection $$P$$.

Après un grand nombre de multiplications avec elle-même, c’est-à-dire 20-30, la matrice se réduit à des valeurs diagonales de $$\lambda$$, appelée valeur propre dominante de la matrice de projection $$P$$. Puisque $$P^n$$ est une matrice diagonale, nous pouvons la remplacer par $$\lambda^n$$.

$$P_n = \begin{bmatrix} \lambda^n & 0 & 0 \\ 0 & \lambda^n & 0 \\ 0 & 0 & \lambda^n \end{bmatrix}$$

Équation 5

La structure démographique devient stable ; les rapports entre les éléments vectoriels sont constants. Le vecteur population stabilisée devient le vecteur propre. Nous pouvons normaliser le vecteur propre à une longueur de $$1$$, que l’on appelle également un vecteur propre normalisé.

---

Références (en anglais)

J.H. Vandermeer and D.E. Goldberg (2003). Population Ecology: First principles. Princeton and Oxford, Princeton University Press.

Shabb et al. (2013). A Mathematical Model of the Dynamics of Mongolian Livestock Populations, in: Livestock Science 157, 280-288.

Lizenz

Downloads